Building Canoe Paddles

[Dana]

That's a great question(s). I'm never quite certain about the term "dihedral" as it pertains to paddle blades, as I would presume that almost all blades are "dihedral" unless each face is completely flat, i.e., the same thickness from edge to edge. Camber, on the other hand, refers to the curvature of the blade, from edge to edge, being thicker in the center, therefore convex.
My blades are all gently cambered, thus convex. They also gently taper from thin at the tip to nearly the thickness of the shaft, at the throat. There is no defined "spine" except, perhaps a tiny bit at the throat. Regarding concavity, except for a minimal bit, right art the throat, concavity should be avoided (in my opinion). Any concavity results is turbulence, especially when doing in-water recoveries.
In summary: It is important that the camber on each facet be matched and also be matched on the front and rear faces of the blade. Blades with mismatched camber will not slice cleanly. If there is greater camber on one face of the blade than the other, the blade will tend to "lift" toward the side with greater camber (Bernoulli's principle), when sliced. Any significant spline, will cause turbulence, and thus is to be avoided.

This is an interesting discussion, coming from an aerodynamics background with my first ever homemade paddle roughed out and waiting for my return to the cabin to finish it.

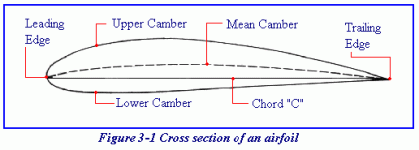
In aircraft wing design, "camber" usually refers to the mean line curvature, which is the average of the upper and lower surface curvature (which are sometimes referred to as the "upper surface camber" and the "lower surface camber"). A symmetrical airfoil (same curvature top and bottom) has zero mean camber; the mean line is a straight line. Airfoils are defined by a thickness distribution (how the thickness varies from front to back, the actual thickness in percent of chord (the length from front to back, typically 10-15%). That thickness distribution is superimposed on the cambered (or straight) mean line to define the upper and lower surfaces.



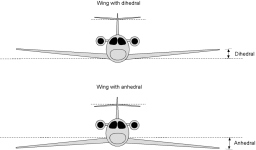
"Dihedral" is an angle, not a curve, referring to the upwards angle of the wings from the center to the tips, viewed from the front to the tips. I could see it applying to the blade faces if they're flat tapered and not curved.

A cambered airfoil will produce lift (which some attribute to Bernoulli, though it's not a simple as that) unless it's angled nose down to compensate for that, which creates more drag than a symmetrical (uncambered) section producing zero lift. Also if a paddle blade has any mean camber, it will tend to twist when slicing through the water. But there are one sided paddles, no? A cambered blade could be more efficient during the pulling stroke, at the expense of slicing behavior.

 

[Marc Ornstein]

If I understand all of this correctly, my paddles, by your description, have zero mean camber. With some few exceptions, most skilled paddlers (with the exception of many racers and others employing bent shaft paddles) employ a variety of in-water recoveries and loaded slices. The paddle is often palm rolled, thus, what was the power face on one stroke, may become the back face on the next. Anything other than zero mean camber would be, to a greater or lesser extent unpredictable, inefficient, and frustrating to use.
I don't follow your comment "A cambered blade could be more efficient during the pulling stroke, at the expense of slicing behavior." Perhaps I don't follow your meaning. Except for some virtually flat boards, passed off as paddles at the big box stores, almost all if not all paddles that I've ever come across are cambered, at least on one face. For example, bent shaft paddles are commonly flat on the power face and cambered on the rear. Your take on this?

 

[Dana]

The paddle is often palm rolled, thus, what was the power face on one stroke, may become the back face on the next. Anything other than zero mean camber would be, to a greater or lesser extent unpredictable, inefficient, and frustrating to use.

Exactly.

I don't follow your comment "A cambered blade could be more efficient during the pulling stroke, at the expense of slicing behavior." Perhaps I don't follow your meaning. Except for some virtually flat boards, passed off as paddles at the big box stores, almost all if not all paddles that I've ever come across are cambered, at least on one face. For example, bent shaft paddles are commonly flat on the power face and cambered on the rear. Your take on this?

What I meant was, if there is some amount of mean camber (front face different from the back face), then it becomes a one sided paddle (like the bent shaft paddles you mentioned). You wouldn't palm roll such a paddle and it wouldn't behave well during slicing, but it could give you more power when pulling, at the expense of versatility... compare pushing an open cup through the water with open side forward vs. open side facing back; open side back will give you more thrust. Different paddles for different uses, and different paddler preferences.

But I'm only talking from fluid mechanics theory, I know little about the state of the art in paddle design... but I can see that it's an interesting subject, and a potentially very deep rabbit hole.

 

[gumpus]

But I'm only talking from fluid mechanics theory, I know little about the state of the art in paddle design... but I can see that it's an interesting subject, and a potentially very deep rabbit hole.

Another fun subject that's a little off the main topic. While things always get interesting when you take a really close look I'll stick my neck out and say most or all of the top paddles do a whole bunch of things the same. Take a look at the Zaveral Power Surge...even that highly specialized paddle with a scoop blade has a strong center ridge (dihedral? fatterinthemiddleness?) to stabilize the blade (blades with flat power faces can flutter under power), sharp edges (for many good reasons), and smooth changes in geometry (no discontinuities). And there are exceptions and great potential for endless debate around how sharp is sharp, how much fatterinthemiddleness us ideal, ...).

 

[Glenn MacGrady]

In aircraft wing design, "camber" usually refers to the mean line curvature, which is the average of the upper and lower surface curvature (which are sometimes referred to as the "upper surface camber" and the "lower surface camber"). A symmetrical airfoil (same curvature top and bottom) has zero mean camber; the mean line is a straight line. Airfoils are defined by a thickness distribution (how the thickness varies from front to back, the actual thickness in percent of chord (the length from front to back, typically 10-15%). That thickness distribution is superimposed on the cambered (or straight) mean line to define the upper and lower surfaces.

"Dihedral" is an angle, not a curve, referring to the upwards angle of the wings from the center to the tips, viewed from the front to the tips. I could see it applying to the blade faces if they're flat tapered and not curved.

I suspect both "camber" and "dihedral" are words borrowed by the canoe paddle world from the airplane world.

Note from @Dana's diagram above that even symmetrical camber, creating a zero mean camber line, still produces a teardrop shape from the front of the airfoil wing to the back. The frontal cross-section of a canoe paddle blade would not have such a tapered or asymmetrical camber from side-to-side, even if the camber is symmetrical with respect to the power and back faces. The paddle blade camber has to be symmetrical not only on both faces but also on each side of the central spine. That's where the word "dihedral" may have come in.

Here's an illustration of airplane wing dihedral angle, which is the angling up of the wings from the central fuselage. An angling down from the fuselage is called an anhedral angle. Analogizing, one can think of the airplane fuselage as the central spine of the paddle blade.



From the illustrations of airplane wing camber and dihedral, one can see how someone applied those words to the cross-section of a canoe paddle blade.

Using these terms properly, perhaps one should say that Marc's paddle blades have symmetrical camber on both faces, and the camber is also symmetrically dihedral from side-to-side on both faces. (To get really technical, I suppose the camber on one face would be symmetrically dihedral and the camber on the other face would be symmetrically anhedral.)

"Dogpaddle: Where, in our secret bed, we router your face to have symmetrical anhedral and dihedral angles and a zero mean camber line! No Botox involved."

A short term that captures all of the above is a paddle blade that is "symmetrically foiled."

 

[Woodpuppy]

I’m more familiar with “dihedral” referring to birds’ wings. A vulture has a pronounced dihedral, but eagles, falcons, and hawks do not. It helps in identifying them by silhouette when backlit or what have you. Gliding birds have a dihedral, fast birds do not.

 

[Glenn MacGrady]

compare pushing an open cup through the water with open side forward vs. open side facing back; open side back will give you more thrust.

Not sure about this analogy, but water tank testing has been done on canoe paddles to compare flat power faces, positively cambered (convex) faces, and negatively cambered (cupped or curved) power faces.

Curved power faces are the most powerful. They hold a "puddle" of water within them as they are pulled through the water. Consequently, they don't shed water easily off the power face and are the most subject to "flutter." Curved power faces are very common in straight shaft whitewater paddles and in flat water racing bent shaft paddles, situations in which many padders want maximum power per pull and arent concerned about flutter, slicing or palm rolling.

As @gumpus points out, some cupped/curved paddles have a dihedral spine down the middle of the power face, creating negatively cambered (concave) pockets on each side of the central spine. The ZRE Power Surge blade has this architecture, as did the earlier, straight shaft Sawyer Stingray, designed by Harold Deal and Bob Foote, and the bent shaft Sawyer Manta.

Flat power faces are the next most powerful and they shed water in random ways. Hence, they are also subject to flutter. Many recreational bent shafts and older racing bent shafts have flat power faces. Again, paddlers don't palm roll or slice bent shafts. They want efficient power for high stroke rate paddling or for long distance forward stroke cruising.

For an all-around straight shaft paddle that sheds water cleanly, flutters least and slices best, a symmetrically foiled blade like Marc's Dogpaddles are condidered by most experienced paddlers to be the best. The slight loss of power is of little to no significance to most non-racing recreational canoeists, trippers and freestylers. Predictable paddle control using either face of the paddle is of higher priority.

 

[Marc Ornstein]

Exactly.

What I meant was, if there is some amount of mean camber (front face different from the back face), then it becomes a one sided paddle (like the bent shaft paddles you mentioned). You wouldn't palm roll such a paddle and it wouldn't behave well during slicing, but it could give you more power when pulling, at the expense of versatility... compare pushing an open cup through the water with open side forward vs. open side facing back; open side back will give you more thrust. Different paddles for different uses, and different paddler preferences.

But I'm only talking from fluid mechanics theory, I know little about the state of the art in paddle design... but I can see that it's an interesting subject, and a potentially very deep rabbit hole.

Dana, Thanks for that clarification. Seems like we were talking the same language, only with different dialects.

 

[Marc Ornstein]

Once the rough cutting is done, it's necessary to refine the shape of the tip, as shown here. This is done by eye, on a stationary belt sander. It's necessary to keep a close watch on several reference points so that everything stays symmetrical. Essentially, it's "thinning the camber" at and near the tip, equally on both sides. A thin, refined, tip knifes cleanly into the water, at the catch of each stroke.